202307_业务-材料科学和计算机模拟
none
20230717:创建文档计算机模拟 主要用于 解释实验机理以及预测实验
GNN物性预测
GNN, 即图神经网络(Graph Neural Networks), 一种专门处理图形数据的神经网络模型
晶体结构
在晶体结构中, 通过 原子的特征(如原子类型, 原子坐标等) 和 化学键的特征(键的类型, 键的长度), 预测晶体的物性
| 输入数据 | 预测数据 | 名词解释 |
|---|---|---|
| 原子类型 | 形成能 | 元素最稳定状态形成目标化合物的能量 |
| 元组坐标 | 能带间隙 | 导带和价带之差, 存在能带间隙则无法直接导电 |
| 键的类型 | 费米能级 | 费米能级在零绝对温度下对应于最高占据的电子能级。 |
| 键的长度 | 体积模量 | 表征材料抗压能力 |
| 剪切模量 | 描述固体材料对剪切变形的抵抗能力 |
剪切力: 剪切力会使物体的一部分相对另一部分产生滑动,
QE(量子化学计算软件包)
主要用于 固体 电子结构和性质 的计算 , 是一个开源的量子化学计算软件包
| Items | 原理 | 作用 |
|---|---|---|
| QE结构优化 | 通过QE找到分子或者晶体中最稳定的原子结构 | 通过改变晶体中原子的位置和形状, 以达到能量最低点, 已找到材料真实的最优结构 |
| QE单点能计算 | 根据原子位置和形状, 计算材料的电子结构和总能量 | 判断原子结构稳定性, 确认结构优化是否为最优结构 |
| QE能带结构分析 | 用于计算固体材料的能带结构, 确认材料的导电性质 | |
| QE态密度DOS | 态密度: 在给定的能量范围内, 单位体积和单位质量的材料中存在的电子能级数 | 获得材料的电子能级分布情况 |
| QE光学性质 | 通过材料的基态电子密度和能带结构, 计算折射率 | 用于计算 材料的光吸收和折射率性质 |
| QE声子计算 | 声子是材料中虚构的震动粒子, 用来表征材料原子在外力和能量下震动行为 | 用于计算声子态密度, 提供 热传导, 相变等信息 |
Gaussain
高斯函数: 表征一种钟型曲线, 最大值取决于u, A决定振幅,σ 是标准差
$$
f(x) = A \cdot e^{-\frac{(x - \mu)^2}{2 \sigma^2}}
$$

高斯函数曲线
| Items | 原理 | 作用 |
|---|---|---|
| 高斯结构优化 | 通过高斯函数计算几何构型能量获得获得最优结构 | 通过改变晶体中原子的位置和形状, 以达到能量最低点, 已找到材料真实的最优结构 |
| 高斯电子能计算 | 判断原子结构稳定性, 确认结构优化是否为最优结构 | |
| 高斯自旋密度 | 计算分子或材料体系中的自旋密度分布。自旋密度是描述电子自旋分布的物理量 | 计算自旋密度, 用于研究分子或材料的磁性行为和反应机制 |
| 高斯分子轨道计算 | 分子轨道波函数通常被表示为组成分子的所有原子的原子轨道的线性组合 | |
| 静电势计算 | 静电势是由电荷分布产生的电场在空间中的分布 | 计算材料静电势 |
| 过渡态优化 | 过渡态是指反应中处于最高能量点的状态,是反应物和产物之间的临界状态,同时具有反应物的性质和产物的性质 | 对处于过渡态的结构进行优化,找到能量最高的状态 |
| IRC解析 | 根据过渡态的几何结构,沿着内禀反应坐标方向进行分析,从而得到反应的前进路径和回退路径。 | 在IRC分析结束后,得到了一系列沿着反应路径的几何结构和能量信息,用于理解化学反应过程 |
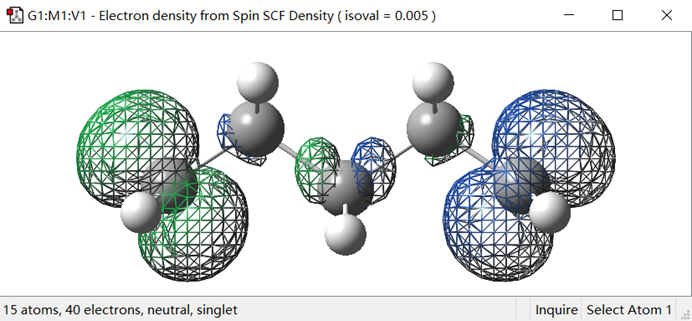
自旋密度图
https://blog.sciencenet.cn/blog-671981-639926.html
氧气: https://www.zhihu.com/question/492055430
结构
| 名词 | 解释 | 如何造数据 |
|---|---|---|
| 自由基 | 拥有未成对电子的反应中间体或者分子, 具有高度反应性 | 分子加H饱和再扣掉H |
自旋复杂度计算
概念
| 名词 | 解释 | 电子构型影响 |
|---|---|---|
| 自旋量子数 | 描述例子绕自身轴旋转的角动量 | 电子的自旋用S表示 , 有上自旋(↑)和下自旋(↓)2个状态, 取值为+1/2和-1/2 |
| 泡利不相容原理 | 着每个电子在同一原子中的四个量子数必须至少有一个不同。 | 搭建起来 1s²2s²pⁿ等电子构型 |
| 能量最低原则 | 电子倾向于填充较低能级的轨道, 到达稳定的结构 | 电子先填充低能级轨道 |
| 洪特规则 | 在填充同一能级(相同主量子数n)的不同轨道(不同角量子数l)时,电子将首先尽量单独地填充每个轨道,直到每个轨道都有一个电子,然后电子才会成对地填充这些轨道。 | 同一能级中, 电子优先单独填充每个轨道 |
泡利不相容原理的四个量子数:
- 主量子数n: 1, 2 , 3… 代表不同的层数
- 角量子数l: s, p, d, f… — 代表不同的轨道 第一层有1个轨道: s, 第二层有2个: s,p 以此类推
- 磁量子数m: l, l-1 , …. , 0, l+1, l — 代表不同的方向 s只有1个0 , 而 o 有3个: -1,0,1 , 以此类推
- 自旋量子数s: +1/2, -1/2 — 代表不同的自旋方向 1s轨道,有1个方向, 可以填充2个电子; 2p轨道, 有3个方向., 可以填充2*3= 6 个电子

电子构型示意图
计算方法
原子
- 根据外层电子排布, 画出轨道表示式, 得到未成对电子数
- S=N/2, 自旋多重度等于单电子数+1。
离子:
- 画出原子轨道表示式后, 加入或减去外层对应电子, 得到离子轨道表示图( 不确定的话百度可以得到)
- 自旋多重度等于单电子数+1。
参照:

